在频率变换（3）里，我们证明了频率变换（1）里直觉性的推导实际上是充分必要的解。基于我们的证明，我们提出了几种基本的从低通滤波器衍生其他三种高通，带通和带阻滤波器的方法。

除了这三种简单的频率变换之外，这一节我们讨论几种特殊的频率变换方法。

理查变换 (The Richard’s Transformation)

假如说我们想要把一个低通滤波器变成一个带通滤波器，但是这个带通滤波器要有周期性响应，如下图：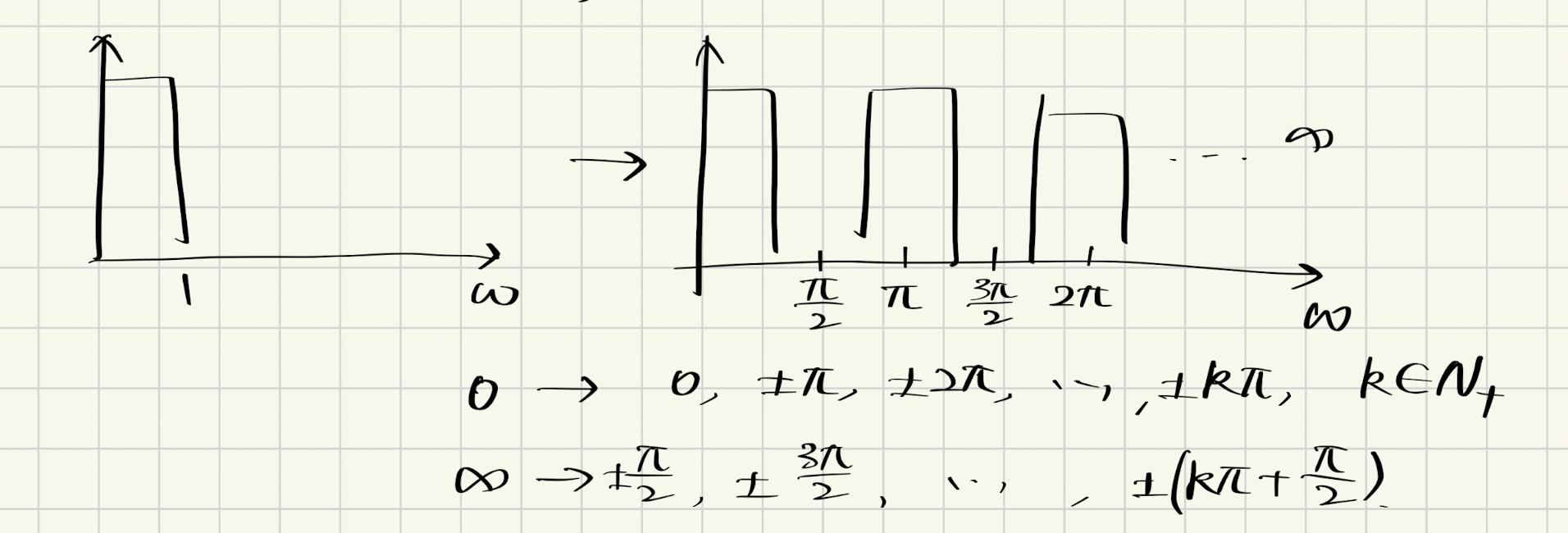

在图中，我们将原本带宽为1 rad/s的低通滤波器变换为中心频率为π，2π…以及π的整数倍的带通滤波器。我们该如何实现这种滤波器？

根据频率变换（1）里讲的两条基本原则：

1. 零点映射：$\omega = 0$必须移动到$f(\omega) = 0$，也就是说$\omega$的零点必须移动到$f(\omega)$的零点
2. 极点映射：$\omega = \infty$必须移动到$f(\omega) = \infty$，也就是说$\omega$的极点必须移动到$f(\omega)$的极点

我们知道，这个变换的零点一定在$0$, $\pm \pi, \pm 2\pi, \ldots, k\pi $的位置上，而变换的极点一定在$\pm \frac{\pi}{2}, \pm \frac{3\pi}{2}, \ldots, (2k+1)\frac{\pi}{2}$的位置上$k \in \mathbb{Z}$。

也就是说，我们的变换应该满足这样的形式：

$$ \begin{aligned}
f(\omega) &= \frac{l \omega (\omega^2 - \pi^2)(\omega^2 - (2\pi)^2)\ldots}{(\omega^2 - (\frac{\pi}{2})^2)(\omega^2 - (\frac{3\pi}{2})^2)\ldots} \\
&= l_1\frac{[\omega(1-\frac{\omega}{\pi}^2)(1-\frac{\omega}{(2\pi)}^2)\ldots(1-\frac{\omega}{(k\pi)}^2)]}{[(1-\frac{\omega}{(\frac{\pi}{2})}^2)(1-\frac{\omega}{(\frac{3\pi}{2})}^2)\ldots(1 - \frac{\omega}{k\pi + \frac{\pi}{2}}^2)]}
\\
&= l_1 \frac{\displaystyle\prod_{k=0}^{\infty}\omega(1 - \frac{\omega}{(k\pi)}^2)}{\displaystyle\prod_{k=1}^{\infty}(1 - \frac{\omega}{(k\pi + \frac{\pi}{2})}^2)}
\end{aligned} $$

实际上，如果我们绘制分子这个无限乘积，它看起来就像：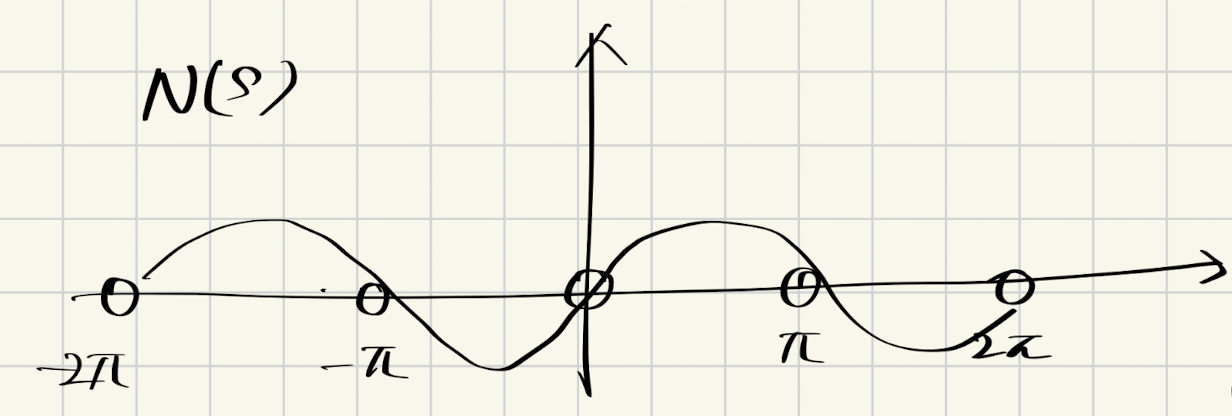

事实上，欧拉告诉我们这两个无限乘积都是三角函数：

$$ \begin{aligned}
\sin(\omega) &= \prod_{k=1}^{\infty}\omega(1 - \frac{\omega}{(k\pi)}^2) \\
\cos(\omega) &= \prod_{k=0}^{\infty}(1 - \frac{\omega}{(k\pi + \frac{\pi}{2})}^2)
\end{aligned} $$

因此，我们有：

$$ f(\omega) = l_1 \frac{\sin(\omega)}{\cos(\omega)} = l_1 \tan(\omega) $$
如果我们把复频率换回普通的频率：

$$\begin{aligned}
f(s) = f(j\omega) &= jl_1 \tan(\omega) \\
&= jl_1 \tan(\frac{s}{j}) = l_1 \tanh (s)
\end{aligned}
$$
由于我们把$\omega \rightarrow l_1 \tan \omega$, 因此如果截止频率为1，那么新的截止频率满足$1 = l_1 \tan(\omega_{\text{bw}}) $，也就是说如果指定一个新的截止频率，$ s \rightarrow \frac{\tanh s}{\tan \omega_{\text{bw}}}$. 如果我们不想要在$\pi$的通带中心点，我们则可以使用放缩。因此，最后的变换公式为：

$$ s \rightarrow \frac{\tanh \frac{s\pi}{\omega_{0}}}{\tan \omega_{\text{bw}}} $$

电路实现

为了简单起见，我们不改变截止频率，只改变中心频率，那么$ s \rightarrow l_1 \tanh \frac{s\pi}{\omega_{0}} $. 在此变换下，一个电感$sL$将会变换成一个$Ll_1\tanh(\frac{s\pi}{\omega_{0}})$.那么问题来了，我们真的有这样一个电子元件可以实现$\tanh$的频率响应特性吗？

传输线(Transmission Line)理论

这个电路就是我们熟知的传输线，如果读者对射频电路有所了解的话。
一个传输线由两个平行导体和一个介质组成，信号在传输线中传播时，会在导体之间形成电场和磁场，从而实现信号的传输。传输线的特性阻抗与其几何结构和介质材料有关。波方程告诉我们，传输线需要满足电报员方程，而要满足电报员方程，我们只需要令正向传播的电压与电流和反向传播的电压与电流满足如下关系：

$$
\begin{cases}
V(x) = V^+(x) + V^-(x) \\
I(x) = \frac{V^+(x)}{Z_0} - \frac{V^-(x)}{Z_0}
\end{cases}
$$
其中$Z_0$是传输线的特性阻抗（characteristic impedance）。

要描述一段传输线，除了传输线的特性阻抗之外，我们还需要这段传输线的时间差（time delay），这段时间差告诉我们电磁波从传输线的一端发射到另一端所需的时间，通常记为$\tau$。
现在，假如我们在某个点满足传输线方程，我们把考虑的点左移动时间$\tau$，那么正向传播的时间将会被提前$\tau$，反向传播的时间将会被延后$\tau$，但是传输线方程依然需要成立：

$$ \begin{aligned}
V^+ &\rightarrow V^+e^{s\tau_1} \\
V^- &\rightarrow V^-e^{-s\tau_1}
\end{aligned} $$