在上一节中，我们得出了两个关于纯LC电路输入阻抗的重要结论：

1. 阻抗的零点和极点必须位于虚轴上。
2. 阻抗（以及导纳）的留数必须是正实数。

本节将进一步分析纯LC网络阻抗在虚轴上的行为，并探讨频率变换的唯一性与实现方式。

柯西-黎曼方程 (Cauchy-Riemann Equations)

对于复平面上的解析函数 $f(x, y) = u(x, y) + iv(x, y)$，其中 $u(x, y)$ 和 $v(x, y)$ 分别为实部和虚部，柯西-黎曼方程给出了函数解析的必要条件：

$$
\begin{aligned}
\frac{\partial u}{\partial x} &= \frac{\partial v}{\partial y} \\
\frac{\partial u}{\partial y} &= -\frac{\partial v}{\partial x}
\end{aligned}
$$

由于LC网络的阻抗是有理函数，必然满足解析性，因此阻抗也必须满足柯西-黎曼方程。对于 $Z(s)$，有：

$$
\frac{\partial}{\partial \sigma}\Re [Z(\sigma + j\omega)] = \frac{\partial}{\partial \omega}\Im [Z(\sigma + j\omega)]
$$

也就是说，阻抗实部对实频率的变化率等于虚部对虚频率的变化率。

结合上一节的正实性结论，进一步有：

$$
\frac{\partial}{\partial \omega}\Im [Z(\sigma + j\omega)] = \frac{\partial}{\partial \sigma}\Re [Z(\sigma + j\omega)] > 0
$$

并且，如果输入信号频率为实数，阻抗为实数；若频率为纯虚数，阻抗也为纯虚数。因此：

$$
\left.Z(s)\right|_{s=j\omega} = jX(\omega) \quad \therefore \frac{dX(\omega)}{d\omega} > 0
$$

简单验证如下：

• 对于电感：$Z(j\omega) = j\omega L \implies \frac{dX(\omega)}{d\omega} = L > 0$
• 对于电容：$Z(j\omega) = \frac{1}{j\omega C} = \frac{j}{-\omega C} \implies \frac{dX(\omega)}{d\omega} = \frac{1}{\omega^2 C} > 0$

因此，LC网络输入阻抗在虚轴上的导数始终为正。这意味着在虚轴上不可能出现连续的极点或零点，否则会与单调性矛盾。如下图所示：

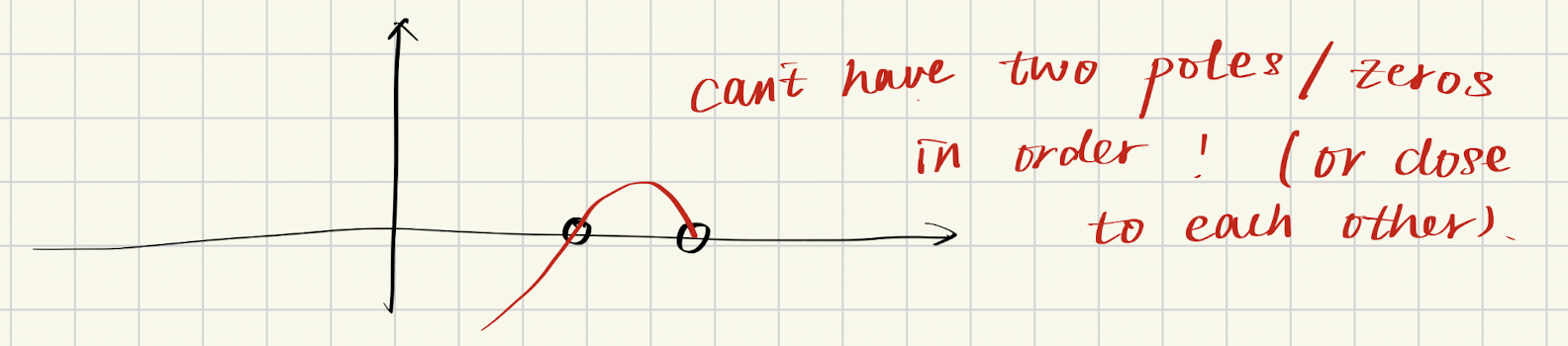
所以，极点和零点在虚轴上必定交替出现：

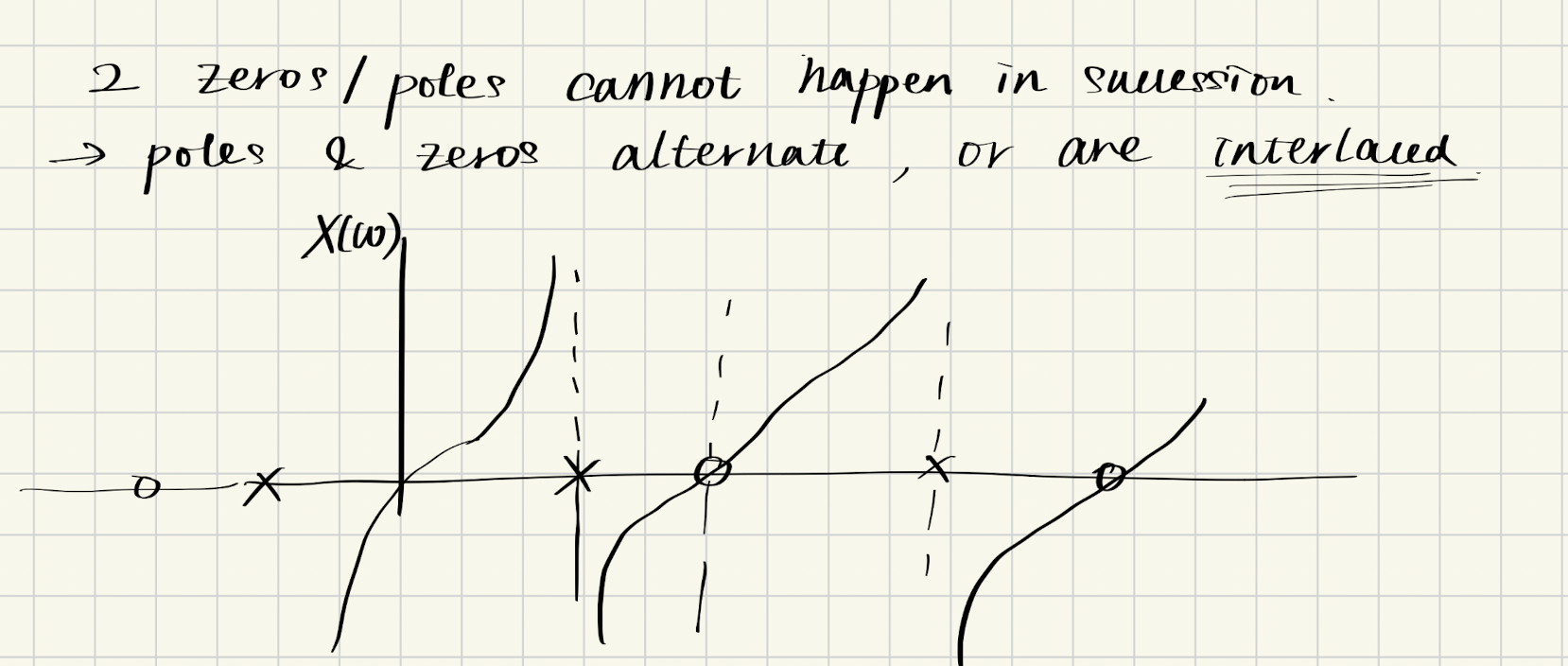
并且，零点数与极点数的差额最多为1。综合所有结论，频率变换的推导实际上是唯一的。

充分必要的频率变换

我们建立了所有需要证明充分性的理论基础，现在是时候来检验我们之前直觉推导的频率变换的唯一性了。

低通-带通变换

低通-带通变换的映射关系如下：

根据频率变换的第一节，变换函数需满足：

$$
f(\omega) \propto \frac{(\omega + 1)(\omega - 1)}{\omega} = \frac{\omega^2 - 1}{\omega}
$$

我们无法引入新的零点，因为差额已经为1.我们也无法引入新的极点。若新的极点为0，那么极点0的重数将不是1.若新的极点模长小于1，将不满足极点-零点交替出现的原则。若新的极点模长为1，将与零点抵消。若新的极点模长大于1，在频率为无穷大的时候的响应就不满足直觉。

由于无法引入新的极点或零点，唯一可调的是比例常数 $K$，且 $K$ 必须为正实数：

$$
f(\omega) = K\frac{(\omega - 1)(\omega + 1)}{\omega}
$$

假设原低通滤波器带宽为 $\omega_{LP}$，则带通滤波器的两个截止频率满足：

$$
\omega_{LP} = K\frac{\omega^2 - 1}{\omega}
$$

舍弃负频率，解得：

$$
\begin{cases}
\omega_a = \frac{\omega_{LP}}{2K} + \sqrt{1 + \frac{\omega_{LP}^2}{4K^2}} \\
\omega_b = \frac{\omega_{LP}}{2K} - \sqrt{1 + \frac{\omega_{LP}^2}{4K^2}}
\end{cases}
$$

有：

$$
\omega_a \omega_b = \omega_{LP}^2 = 1
$$

$$
\omega_a - \omega_b = \frac{\omega_{LP}}{K}
$$

即，两个截止频率的几何平均为中心频率。带通滤波器的品质因子(Q) 定义为：

$$
Q = \frac{\text{Center Frequency}}{\text{Bandwidth}} = \frac{\omega_{LP}}{\omega_a - \omega_b} = K
$$

最终映射为：

$$
s \rightarrow Q\left(\frac{s}{\omega_0} + \frac{\omega_0}{s}\right)
$$

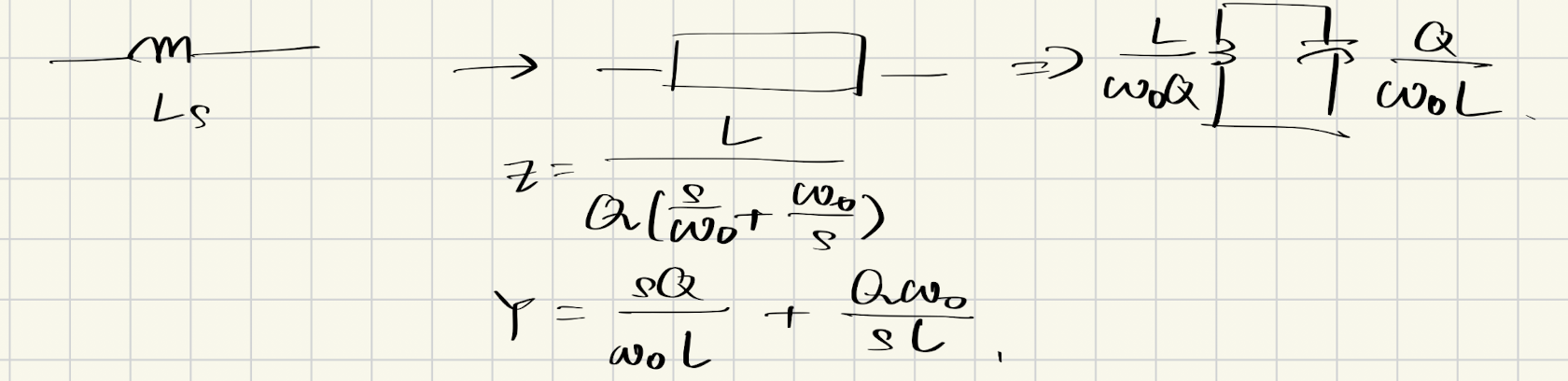
电感的变换：

$$
sL \rightarrow Q\left(\frac{s}{\omega_0} + \frac{\omega_0}{s}\right)L
$$

即，电感 $L$ 变为电感 $\frac{LQ}{\omega_0}$ 与电容 $\frac{1}{QL\omega_0}$ 的串联：

这个结论符合我们的工程直觉，因为在DC的电感时一个短路，而在$\omega_0$的新电路也是短路。无穷频率的电感将是断路，而DC+无穷频率的新电路也是断路。

电容的变换：

$$
C \rightarrow \frac{QC}{\omega_0} \parallel \frac{1}{QC\omega_0}
$$

即，电容 $C$ 变为电容 $\frac{QC}{\omega_0}$ 与电感 $\frac{1}{QC\omega_0}$ 的并联：

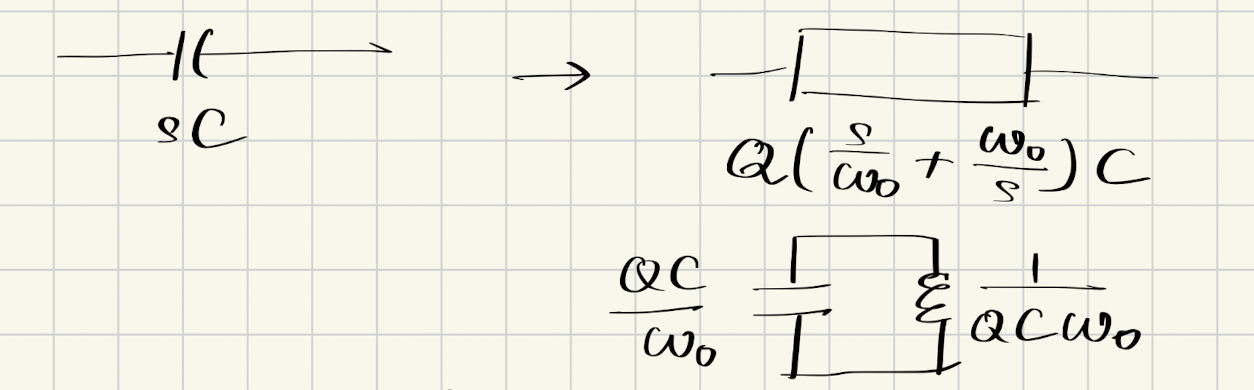
DC的电容是断路，而在$\omega_0$的新电路也是断路。无穷频率的电容是短路，而DC+无穷频率的新电路也是短路。

因此，低通-带通变换后，LC滤波器的阶数翻倍：

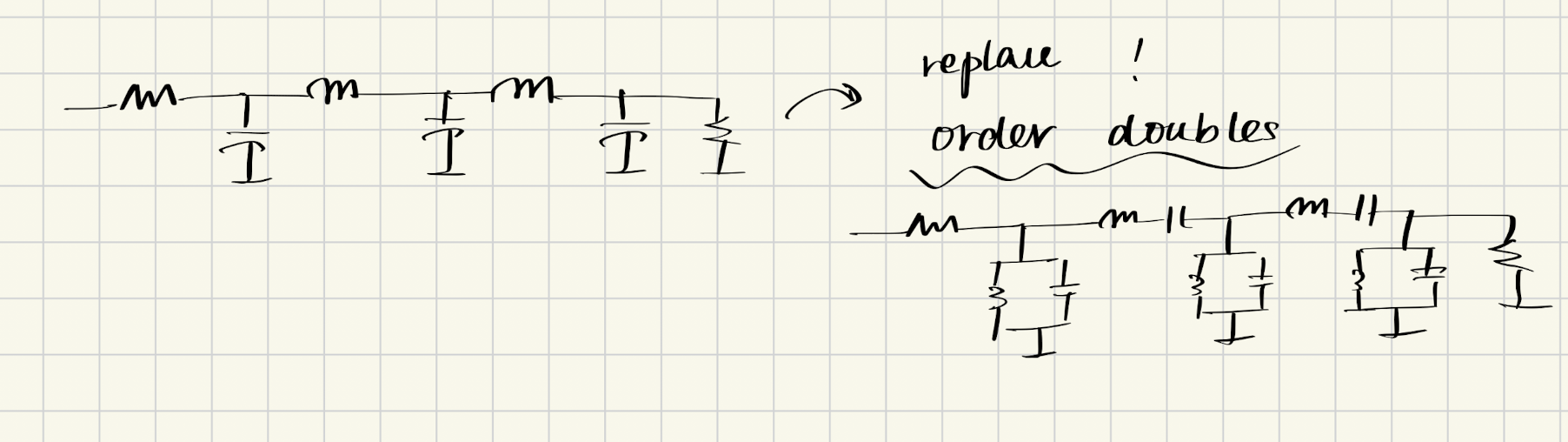
低通-高通变换

低通-高通变换如下：

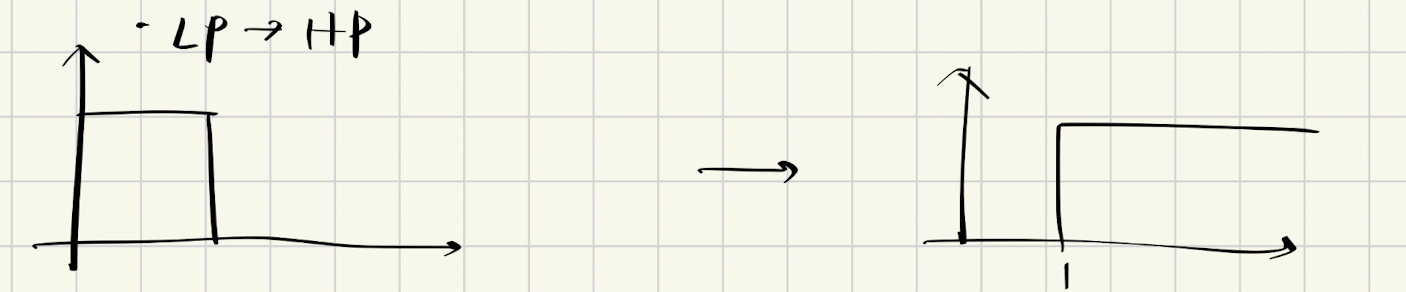
变换关系为：

$$
f(\omega) \propto \frac{1}{\omega}
$$

我们无法引入新的极点，否则零极点差额将会超过1.我们亦无法引入新的零点，否则无穷大的响应将不满足直觉。

因此我们能改变的只有成比例常数：

$$
f(\omega) = \frac{-K}{\omega}
$$

我们一定要引入负号，否则新的阻抗不会是增函数。最终映射为：

$$
j\omega \rightarrow -j\frac{K}{\omega} \rightarrow \frac{K}{j\omega}
$$

若需任意高通频率：

$$
s \rightarrow \frac{\omega_0}{s}
$$

低通-高通变换后，电容变为电感，电感变为电容：

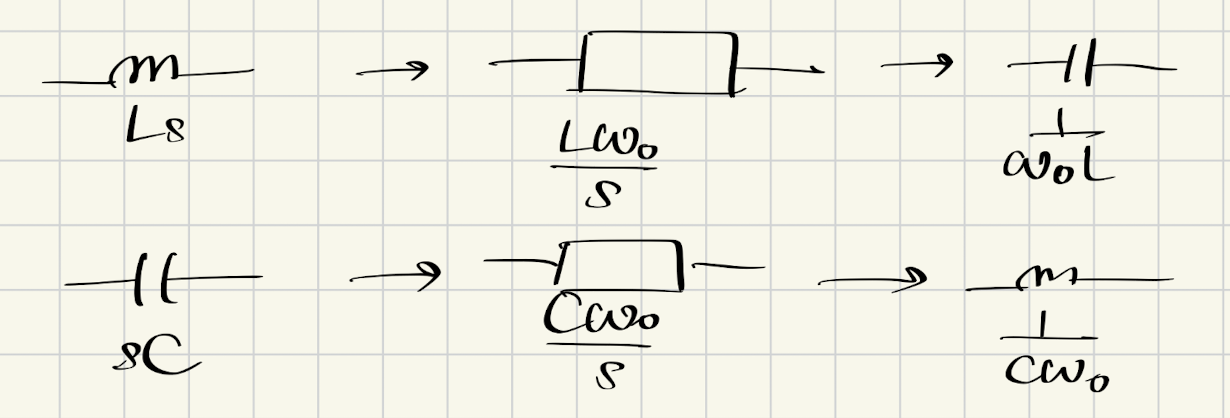
低通-带阻变换

低通-带阻变换如下：

变换关系为：

$$
f(\omega) \propto \frac{\omega}{(\omega + 1)(\omega - 1)} = \frac{\omega}{\omega^2 - 1}
$$

与带通变换一样，我们无法加入任何新的极点或零点。同样，唯一未知量为比例系数，且必须为负实数：

$$
f(\omega) = \frac{-K\omega}{\omega^2 - 1}
$$

带阻滤波器的两个截止频率的几何平均为中心频率，品质因子定义同前。最终映射为：

$$
s \rightarrow \frac{1}{Q\left(\frac{s}{\omega_0} + \frac{\omega_0}{s}\right)}
$$

电感变为电容与电感的并联，电容变为电容与电感的串联：

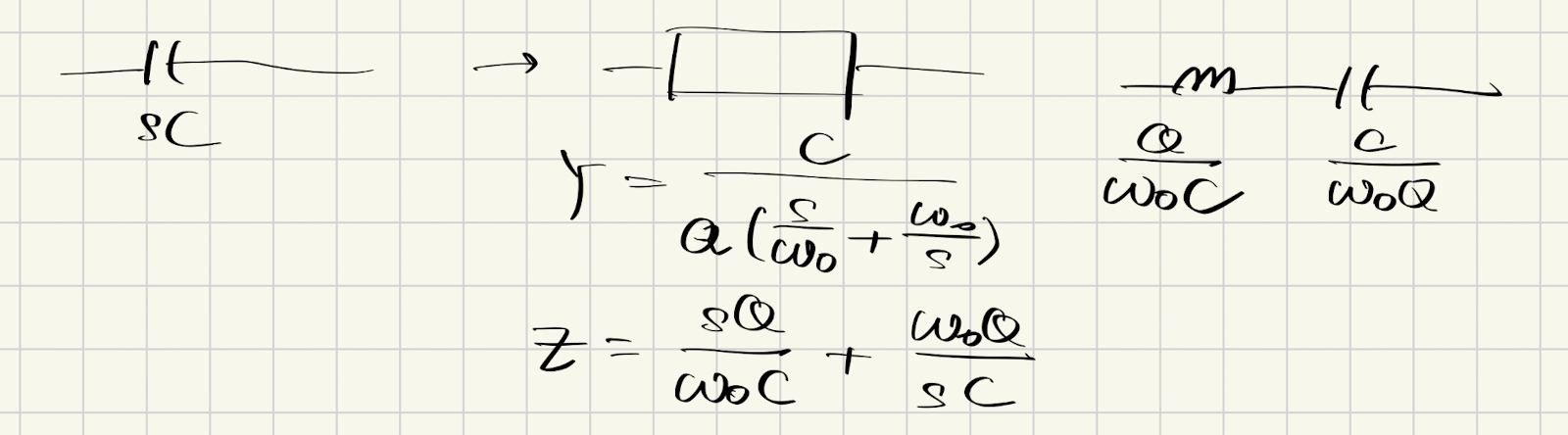
综上，频率变换的形式和参数均由网络的物理特性唯一决定，无法随意添加极点或零点。所有变换均严格遵循正实性和极点零点交替分布的原则。

---

频率变换类型总结表

下表总结了几种从低通出发的频率变换类型及其特性。

变换类型	变换公式	元件变换方式	阶数变化
低通 → 带通	$s \rightarrow Q\left(\frac{s}{\omega_0} + \frac{\omega_0}{s}\right)$	电感 $\rightarrow$ 串联电感+电容 电容 $\rightarrow$ 并联电感+电容	翻倍
低通 → 高通	$s \rightarrow \frac{\omega_0}{s}$	电感 $\rightarrow$ 电容 电容 $\rightarrow$ 电感	不变
低通 → 带阻	$s \rightarrow \frac{1}{Q\left(\frac{s}{\omega_0} + \frac{\omega_0}{s}\right)}$	电感 $\rightarrow$ 并联电感+电容 电容 $\rightarrow$ 串联电感+电容	翻倍

---