tech-主动滤波器(7):频率变换(2)
在上一节中,我们讨论了频率变换的工程直觉。简而言之,频率变换的核心准则只有一条:
零频点应映射到新的零点,无穷频点应映射到新的极点。
基于这一原则,我们通过直觉推导了从低通滤波器到其他类型滤波器的映射关系。然而,这些推导仅能得到“成正比”的关系,属于必要但不充分条件。
本节将进一步探讨纯LC电路的实现特性,并给出充分性证明。
特勒根定理(Tellegen’s Theorem)
在深入分析任何网络之前,我们先引入特勒根定理,为后续推导提供新的数学工具。
考虑如下图所示的网络,底部节点接地,各节点已标注电压与电流。每条支路可包含任意被动或主动元件,且可能为线性或非线性。
我们约定如下:
- 电流方向:流入节点为正,流出为负。
- 电压极性:高电位端为正,低电位端为负。
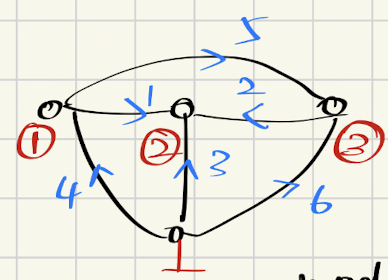
首先,我们可在节点1、2、3建立KCL方程,或用矩阵形式表示:
$$\begin{bmatrix}
-1 & 0 & 0 & 1 & -1 & 0 \\
1 & 1 & 1 & 0 & 0 & 0 \\
0 & -1 & 0 & 0 & 1 & 1
\end{bmatrix} \begin{bmatrix}
i_1 \\ i_2 \\ i_3 \\ i_4 \\ i_5 \\ i_6
\end{bmatrix} = \begin{bmatrix}
0 \\ 0 \\ 0
\end{bmatrix} $$
记为 $\textbf{A}\textbf{I} = \textbf{0}$。
这一关系总是成立,否则电流将无故产生或消失,违背物理定律。$\textbf{A}$ 的每一行对应一个节点的KCL,每一列对应一条支路的电流方向。
定义支路电压(Branch Voltage)为第n支路的电压,例如支路1的电压为 $V_1 - V_2$。构建支路电压向量,满足:
$$ \textbf{V}_B = - \textbf{A}^T \textbf{V} $$
以本例验证:
$$\textbf{V}_B=\begin{bmatrix}
V_1 - V_2 \\
-V_2 + V_3 \\
-V_2 \\
-V_1 \\
V_1 - V_3 \\
-V_3
\end{bmatrix} = -\begin{bmatrix}
-1 & 1 & 0 \\
0 & -1 & 1 \\
0 & 1 & 0 \\
1 & 0 & 0 \\
-1 & 0 & 1 \\
0 & 0 & 1 \end{bmatrix} \begin{bmatrix}
V_1 \\
V_2 \\
V_3 \end{bmatrix}
= -A^T V $$
由能量守恒,有:
$$ \textbf{V}_B^T \textbf{I} = 0 $$
或展开为:
$$ \sum_k v_{bk}i_k = 0 $$
证明如下:
$$
\begin{aligned}
\textbf{V}_B^T \cdot \textbf{I} &= (-A^T \textbf{V}_B)^T \cdot \textbf{I} \\
&= -\textbf{V}_B^T A \cdot \textbf{I} \\
&= -\textbf{V}_B^T \cdot \textbf{0} \\
&= 0
\end{aligned}
$$
上述推导基于KCL和KVL,并未假设元件类型或线性特性。特勒根定理进一步指出,即使支路电流和支路电压分别对应不同网络的元件,这一广义能量守恒关系依然成立。
考虑如下两个网络,A与B实现方式完全不同,A可能由电容、电感组成,B则可能包含主动源或其他元件。
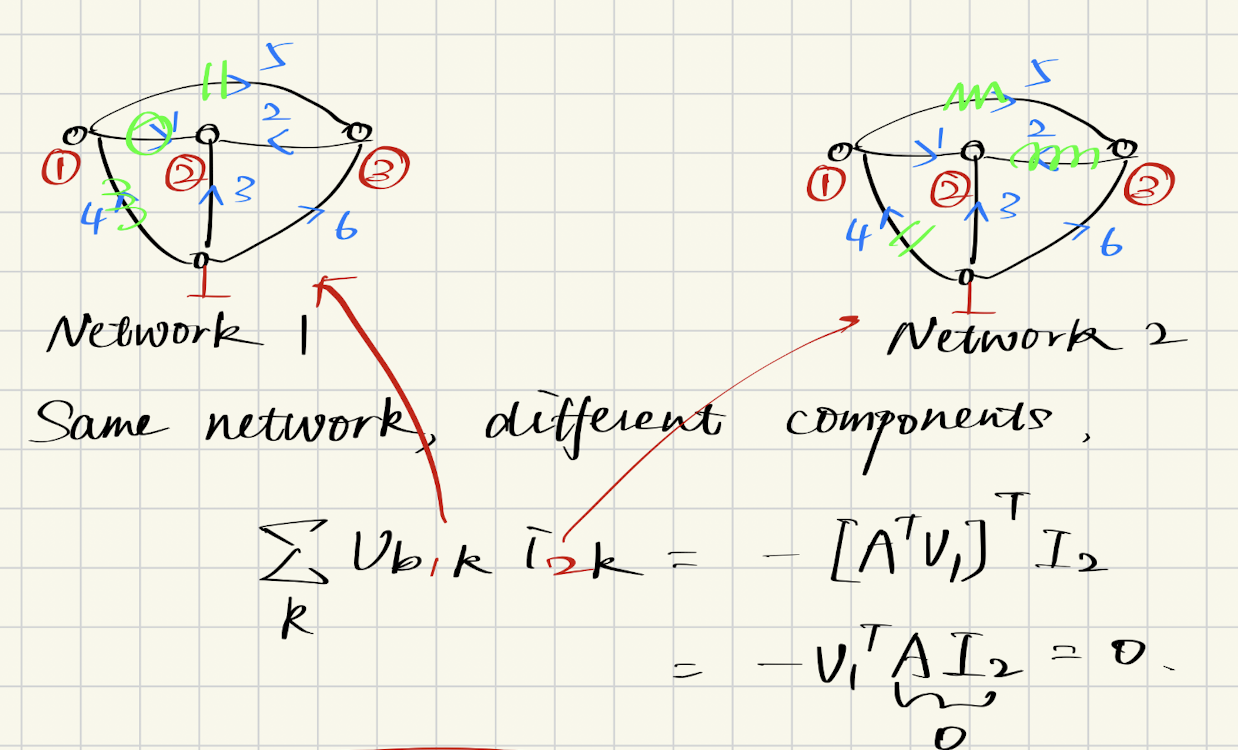
同样有:
$$
\begin{aligned}
\sum_k{v_{b1k}i_{2k}} &= - [A^T \textbf{V}_1]^T \textbf{I}_2 \\
&= - \textbf{V}_1^T A \cdot \textbf{I}_2 \\
&= - \textbf{V}_1^T \cdot \textbf{0} \\
&= 0
\end{aligned}
$$
这一结论极具普适性,表明只要网络结构相同,无论元件如何分布,广义能量守恒都成立。该定理适用于任意线性或非线性电路。
对于感性元件,功率定义为 $P = VI^*$,因此可得:
$$\textbf{V}^T_B \textbf{I}^* = \sum_k v_{bk} i_k^* = 0 $$
LC网络的极点与零点
考虑一个仅由LC元件组成的无损耗网络:
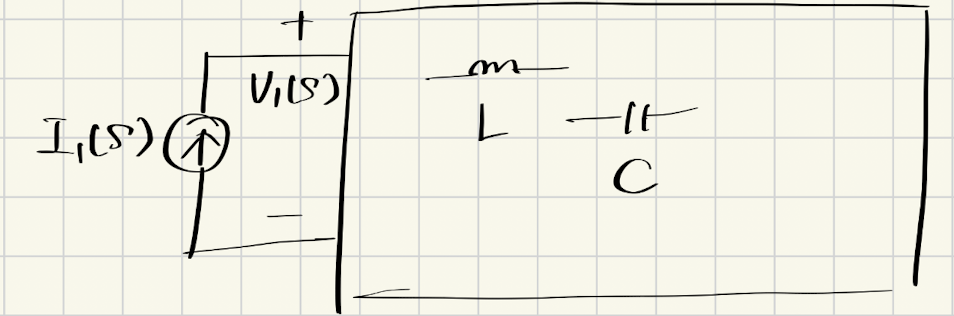
由能量守恒,有:
$$
\begin{aligned}
|I_{1}(s)|^2 Z(s) &=
\sum_{\text{All L and C}} v_k(s) i_k^*(s) \\
&= \sum_{\text{All L}} s L_k i_k(s) i_k^*(s) + \sum_{\text{All C}} \frac{1}{sC_k} i_k(s) i_k^*(s) \\
&= \sum_{\text{All L}} s L_k |I_k(s)|^2 + \sum_{\text{All C}} \frac{1}{s C_k} |I_k(s)|^2
\end{aligned}
$$
令 $I_1(s) = 1$,则
$$
\begin{aligned}
Z(s) &= \sum_{\text{All L}} s L_k |I_k(s)|^2 + \sum_{\text{All C}} \frac{1}{sC_k} |I_k(s)|^2 \\
&= \sum_{\text{All L}} s P_1 + \sum_{\text{All C}} \frac{1}{s} P_2
\end{aligned}
$$
其中 $C$, $L$, $|I|^2$ 均为正实数,因此 $P_1, P_2 > 0$。
由此可得两点结论:
- 若频率变量 $s$ 为实数,则 $Z(s)$ 也为实数。
- 若 $s$ 有正实部,则 $Z(s)$ 的实部也为正。
我们将满足此性质的函数称为正实函数(Positive Real Function)。即对于仅含L和C的网络,有:
$$
\Re{[Z(s)]} \begin{cases} > 0 \text{ if } \Re[s] > 0 \\ = 0 \text{ if } \Re[s] = 0 \\ < 0 \text{ if } \Re[s] < 0
\end{cases}
$$
复变函数的极点行为观察
观察复变函数在极点附近的行为。以 $\frac{1}{s - p_1}$ 为例,在极点 $p_1$ 左侧,函数实部为负;在右侧,实部为正。
若引入带有相位的留数(Residue),则分界线会随留数相位旋转。例如,绘制 $\frac{\angle 45^{\circ}}{s}$ 的实部分布:
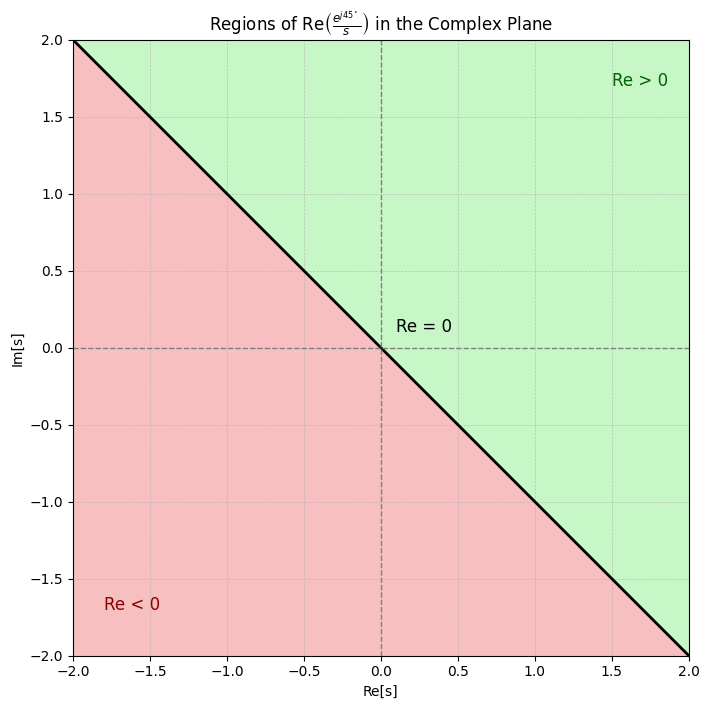
若极点为重复极点,如 $\frac{1}{s^2}$,其实部分布如下:
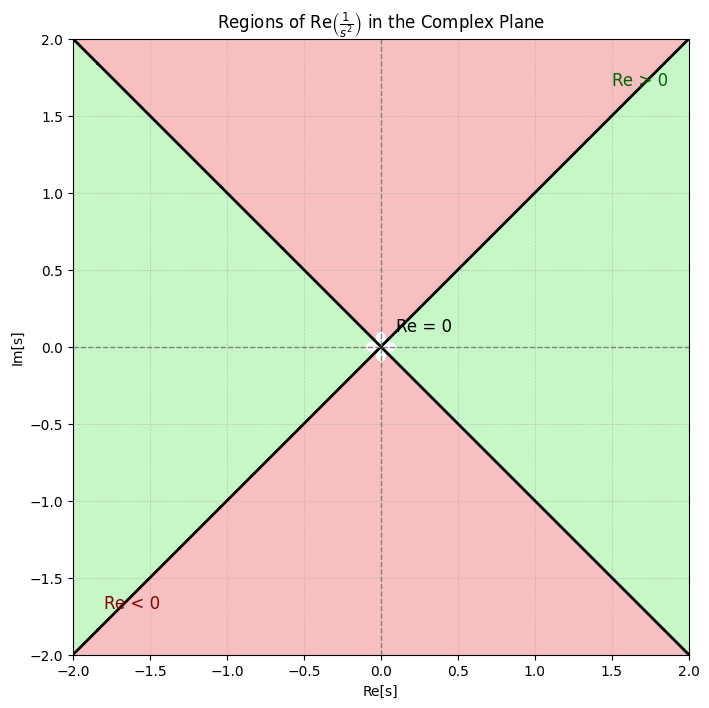
而我们期望的函数实部行为应如下图所示:
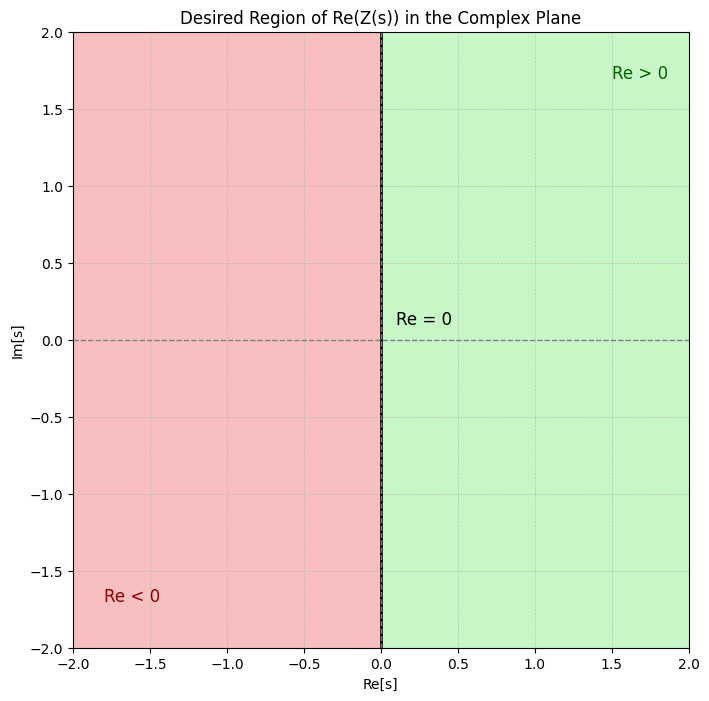
因此,为使函数实部符合预期,需满足以下条件:
- 无左半平面极点,否则分界线将不在虚轴。
- 无右半平面极点,同理。
- 虚轴上的极点必须为简单极点(重数为1),否则分界线将非对称分割复平面。
- 留数必须为正实数,否则分界线将发生旋转。
此外,实系数函数的极点必以共轭对出现。上述讨论对导纳同样适用,因此零点也满足类似约束。
下一节将进一步探讨LC网络在虚轴上的零极点分布。