tech-主动滤波器(5):双端LC滤波器(2)
在上一节中,我们解释了如何使用双端LC滤波器的标准形式来设计一个全极点滤波器。总结起来,我们有以下的设计流程:
- 设计传递函数$H(j\omega)$
- 进行各种归一化假设
- 通过$H(j\omega)$推导反射系数$\Gamma(s)$
- 通过$\Gamma(s)$推导输入阻抗$Z_{in}(s)$
- 通过$Z_{in}(s)$推导整个滤波器的电路结构
我们知道,使用双端LC滤波器的标准形式,输入阻抗可以表示为:
$$Z_{in}(s) = sL_1 + \cfrac{1}{sC_1 + \cfrac{1}{sL_3 + \cfrac{1}{\ddots}}}$$
这是一个有限的连分数形式。我们可以通过这个公式推导出$Z_{in}(s)$,从而得到滤波器的电路结构。
本节将对LC标准形式进行总结,并讲解一些特殊情况的处理方法。
1. 全极点LC滤波器的性质
双端LC滤波器具有以下重要性质:
- 反射系数特性:在通带内,反射系数几乎为0;在阻带内,反射系数接近1
- 零点特性:在传递函数的零点处,反射系数为0
- 阶数限制:使用LC标准形式,我们只能实现传递函数的分子和分母阶数差不超过1的滤波器
- 这是因为在频率趋近于无穷时,输入阻抗只能表现为L、R、C中任意一种形式的特性
- 可实现的滤波器类型:
- 奇数阶或偶数阶巴特沃斯滤波器
- 奇数阶第一类切比雪夫滤波器
- 无法实现偶数阶第一类切比雪夫滤波器,因为其直流增益不等于1/2
那么,我们能否实现第二类切比雪夫滤波器?答案是肯定的,但需要对双端LC标准形式做适当的改进。
2. 第二类切比雪夫滤波器的电路实现
2.1 有限零点与谐振回路
第二类切比雪夫滤波器具有有限零点,而标准的双端LC形式只能实现全极点滤波器。因此,仅使用标准形式无法插入有限零点,从而无法实现第二类切比雪夫滤波器。
解决方案是引入谐振回路(Resonant Tank) 。
并联谐振回路
并联谐振回路的结构如下:
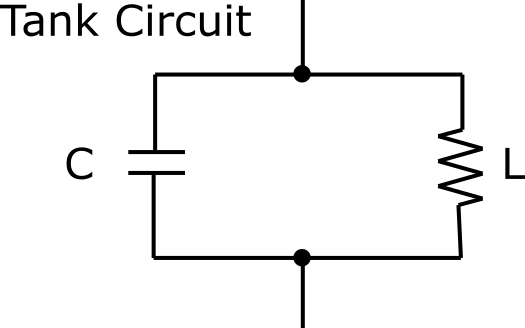
对于并联谐振回路,其输入阻抗为:
$$Z_{in}(j\omega) = \frac{1}{j\omega C} \parallel j\omega L = \frac{j\omega L/C}{1 - \omega^2 LC}$$
串联谐振回路
对于串联谐振回路,其输入阻抗为:
$$Z_{in}(j\omega) = j\omega L + \frac{1}{j\omega C} = -j\frac{1 - \omega^2 LC}{\omega C}$$
谐振特性
在$\omega = \frac{1}{\sqrt{LC}}$时:
- 串联谐振回路的阻抗为0
- 并联谐振回路的阻抗为无穷大
这个特殊的角频率称为**谐振频率(Resonant Frequency)**。利用谐振回路的这一特性,我们就可以在滤波器中插入有限零点。
2.2 设计实例:三阶第二类切比雪夫滤波器
让我们尝试实现一个三阶第二类切比雪夫滤波器,使用如下电路结构:
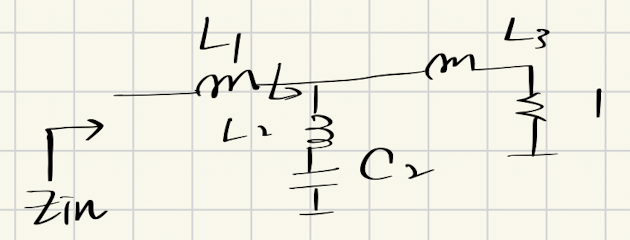
2.2.1 输入阻抗函数
三阶第二类切比雪夫滤波器对应的输入阻抗为:
$$Z_{in}(s) = \frac{2s^3 + 0.6746s^2 + 0.2271s + 0.0400}{0.6746s^2 + 0.2271s + 0.0400}$$
设计提示 (Shanthi Pavan): 当设计具有无理系数的滤波器时,舍入规则的经验法则是保持有效数字位数等于滤波器的阶数。例如,三阶滤波器应保留3位有效数字。否则,舍入误差会在求解电路其余部分时产生负阻抗。
2.2.2 高频特性分析
在无限频率时,由于电容短路,电感占据阻抗的主导地位,因此:
$$L_1 + L_2 \parallel L_3 = \frac{2}{0.6746}$$
2.2.3 零点条件
由于$Z_{in}(s) = sL_1 + Z_{in1}(s)$,我们需要确保在传递函数的零点处,串联谐振回路的阻抗为0。
这样设计的原因有两个:
- 在传递函数的零点处,反射系数为0
- 当谐振回路将剩余阻抗全部短路时,所有输入能量都被反射,负载端电压为0
因此,在零点频率$\omega_z$处:
$$Z_{in}(j\omega_z) = j\omega_z L_1$$
通过计算可得:$L_1 = 2.8384\text{H}$
2.2.4 剩余电路分析
去掉$L_1$后,剩余部分的输入导纳为:
$$Y_{in}(s) = \frac{0.6742s^2 + 0.2271s + 0.0400}{0.0852s^3 + 0.0299s^2 + 0.1135s + 0.0400}$$
串联谐振回路的导纳为:
$$Y_{\text{resonant}}(s) = \frac{sC_2}{1 + s^2L_2C_2}$$
在$\omega_z$处,导纳趋近于无穷大,且$\omega_z = \frac{1}{\sqrt{L_2C_2}}$。
关键观察:在接近$\omega_z$时,$Y_{\text{resonant}}(s)$和$Y_{in1}(s)$的行为非常相似:
$$\lim_{s \to j\omega_z} Y_{in1}(s) = \lim_{s \to j\omega_z} Y_{\text{resonant}}(s)$$
由于只有一个未知数,可求得:$C_2 = 5.6745\text{F}$
剩余求解过程比较直接。使用与上一节相同的方法,可求得:$L_3 = 2.838\text{H}$
代入所有值后,剩余阻抗为1Ω,正符合我们的负载预期。
2.3 偶数阶第二类切比雪夫滤波器的局限性
很遗憾,我们无法使用双端LC滤波器实现偶数阶第二类切比雪夫滤波器,因为在频率趋近无穷大时,要求的传递函数值非零,这与LC电路的物理特性相矛盾。
3. 总结
本节完成了对双端LC滤波器标准形式的总结,并介绍了如何使用谐振回路来实现奇数阶第二类切比雪夫滤波器。
到目前为止,我们的讨论都集中在低通滤波器的设计。读者可能会好奇:我们如何设计其他类型的滤波器——高通、带通、带阻滤波器?
在接下来的章节中,我们将展示一种优雅的数学变换方法,通过频率变换技术,可以将一个低通原型滤波器等价地转换为其他类型的滤波器。这种方法不仅在理论上具有重要意义,在工程实践中也有广泛应用。